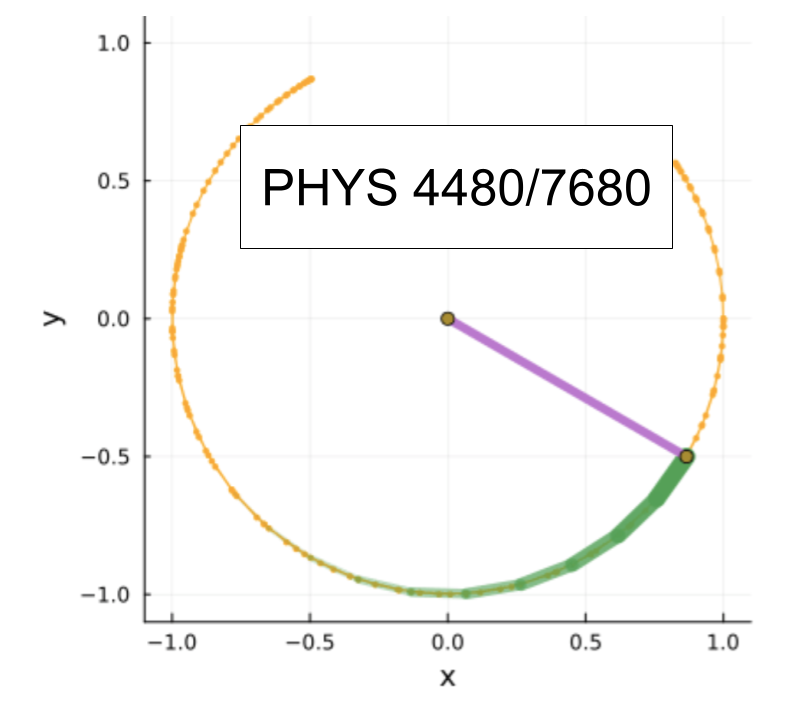
Interactive Animation of Pendulum

Interactive Animation of Pendulum#

As is clear, I find that visualization can be as important as getting numerical answers: If you can’t plot your results, then you can’t get any insight. Earlier we saw one strategy for animating our solution to the differential equation:

  1. Generate time series

  2. Generate animation frames from time series

  3. Assemble frames into a movie

  4. Save the movie to disk

  5. Display the saved movie

The nice thing about that approach is that you can use the same time series for visualization and other analysis. It also gives you a movie to share.

There is a second paradigm, where one generates the frames of the video “on the fly.” You run it until you see something interesting. You don’t have a permanent record, but it is still useful.

The syntax for making a movie in Plots.jl is relatively straightforward. Here we will use Makie.jl to make an interactive animation. The syntax is a bit trickier.

If you just want working animation code – just scroll to the end of this notebook. There is a single cell which contains a self-contained animator for the pendulum.

In the next lab you will apply this approach to the Duffing Oscillator, and try to get more understanding of how chaos works.

Asynchronous Computation#

Another reason for going into this is it introduces an alternate model of computation, asynchronous computation.

So far all of our code has been synchronous, procedural, and linear. The computer steps line-by-line through a program. Executing one command after the next. There can be branching and loops, but one thing leads to the next.

In an asynchronous model, one instead has independent little mini-programs running, which listen for an event. Whenever an event occurs they do something. We will use this to make user interfaces – programs which interact with a user. The interface waits around for human input, and when some occurs it starts some autonomous thread doing something. While that thread is running it still accepts more input.

These Jupyter notebooks are a good example.

I was hoping to use interact.jl to demonstrate this concept, but since it is not working well with the latest Jupyter notebooks, we will instead use GLMakie. This is a OpenGL backend for the Makie plotting program. We earlier saw CairoMakie, which is a different backend. OpenGL is a toolkit (API) for displaying graphics.

One downside of spending time on this is that the exact syntax is somewhat specialized. If we learn the commands to use GLMakie, those same commands will not work in a Python or Javascript. Nonethless the general architecture of all of these interfaces tend to be fairly similar. Moreover concepts are transferable.

If you want to make interactive interfaces which everyone can access using a web browser, you should look into WGLMakie. You may also want to consider writing such things in Javascript – which is a programming language which runs on most web browsers. Javascript is slow, and it is not as fun to program in as Julia.

Code for Solving the differential equation#

Before getting in to using GLMakie, we should set up some of the actual computational infrastructure. We are going to make a program which animates a pendulum – and allows us to interact with that animation. The actual physics will be really really easy. The hard part is telling the computer how to display things and how to let us interact with it.

We will use our Runge Kutta time stepper – but we can obviously introduce another one. We will write the animation code in such a way that we can just plug in the functions that we are using for our integrator.

function pendulum_dxdt(x,t)
    (theta,v)=x
    return [v,-sin(theta)]
end

function rk4step(x,dxdt,t,deltat)
    k1=dxdt(x,t)
    k2=dxdt(x+k1*(deltat/2),t+deltat/2)
    k3=dxdt(x+k2*(deltat/2),t+deltat/2)
    k4=dxdt(x+k3*deltat,t+deltat)
    return x+(k1+2*k2+2*k3+k4)*(deltat/6)
end

rk4step(;x,dxdt,t,deltat)=rk4step(x,dxdt,t,deltat)

rk4step (generic function with 2 methods)

Generating a Makie Scene#

using GLMakie

# Make an "observable" which will update the figure whenever it is changed
ball= Observable(Point2f(1,0))
#
# Generate Figure
fig = Figure(); display(fig)
ax = Axis(fig[1,1])
scatter!(ax, ball; marker = :circle, strokewidth = 2, 
    strokecolor = :purple,
    color = :black, markersize = 8)
ax.title = "pendulum"
ax.aspect = DataAspect() # Set aspect ratio
xlims!(ax, -1.05, 1.05)
ylims!(ax, -1.05, 1.05)

We can now move the ball around with

ball[]=Point2f(0.5,0.1)

2-element Point{2, Float32} with indices SOneTo(2):
 0.5
 0.1

Lets now disable the zoom feature of Makie

Makie.deactivate_interaction!(ax, :rectanglezoom)
xlims!(ax, -1.05, 1.05)
ylims!(ax, -1.05, 1.05)

Lets add another observable to be the shaft of the pendulum

rod= Observable([Point2f(0, 0), Point2f(0.5, 0.1)])
lines!(ax, rod; linewidth = 4, color = :purple)

Lines{Tuple{Vector{Point{2, Float32}}}}

We can now define a function which sets the pendulum to a particular angle. It will be convenient to feed the vector θv=[θ,v], as that is what is used by our stepper/integrator.

function xycoords(θv)
    θ,v=θv
    return (sin(θ),-cos(θ))
end

function setangle!(θv)
    x,y=xycoords(θv)
    rod[] = [Point2f(0, 0), Point2f(x, y)]
    ball[] = Point2f(x, y)
end

setangle! (generic function with 1 method)

setangle!([pi/2,0])

2-element Point{2, Float32} with indices SOneTo(2):
  1.0
 -6.123234f-17

setangle!([pi/4,0])

2-element Point{2, Float32} with indices SOneTo(2):
  0.70710677
 -0.70710677

At this point it is useful to make an object which stores all of this information

# We will learn more about this construction soon
# An abstract type is a way to group objects together,
# we can then define functions which act on all objects
# that are in a given group.  I am using it here because
# we are going to iterate on our animation software, and 
# I would like to define functions that work on all the different
# varients.  I can give the varients different names,
# but as long as they are all subclasses of the abstract class
# they can use the same methods.
abstract type abstractpendulum end

mutable struct pendulum_basic <:abstractpendulum
    fig #Makie figure object
    ax  #Makie axis object
    ball #Observable corresponding to ball
    rod #Observable corresponding to rod
    θv #vector [θ,v]
    t # current time
    dt # time step
    #
    # The following two things we haven't used yet -- but we will need them for the animation
    step  #the stepper for our differential equation solver -- same syntax as rk4step
    dxdt  #the derivitive rule -- same systax as pendulum_dxdt
    delay #how long to wait between displaying frames
end

# Constructor
# This is the function that you call to create one of these objects
function pendulum_basic(;θv=[pi/4,0.],t=0.,dt=0.01,step=rk4step,dxdt=pendulum_dxdt,delaytime=0.001)
    # Extract positions of pendulum
    θ,v=θv
    x,y=xycoords(θv)
    # Make observables
    ball= Observable(Point2f(x,y))
    rod=Observable([Point2f(0, 0), Point2f(x, y)])
    # Make scene
    fig = Figure(); display(fig)
    ax = Axis(fig[1,1])
    scatter!(ax, ball; marker = :circle, strokewidth = 2, 
        strokecolor = :purple,
        color = :black, markersize = 8)
    lines!(ax, rod; linewidth = 4, color = :purple)
    ax.title = "pendulum"
    ax.aspect = DataAspect() # Set aspect ratio
    xlims!(ax, -1.05, 1.05)
    ylims!(ax, -1.05, 1.05)
    # Set up interactive
    Makie.deactivate_interaction!(ax, :rectanglezoom)
    #Create object
    pendulum_basic(fig,ax,ball,rod,θv,t,dt,step,dxdt,delaytime)
end

function setangle!(p::abstractpendulum,θv)
    p.θv=θv
    x,y=xycoords(θv)
    p.rod[] = [Point2f(0, 0), Point2f(x, y)]
    p.ball[] = Point2f(x, y)
    p
end

setangle! (generic function with 2 methods)

p2=pendulum_basic()

pendulum_basic(Scene (600px, 450px):
  0 Plots
  1 Child Scene:
    └ Scene (600px, 450px), Axis (2 plots), Observable(Float32[0.70710677, -0.70710677]), Observable(Point{2, Float32}[[0.0, 0.0], [0.70710677, -0.70710677]]), [0.7853981633974483, 0.0], 0.0, 0.01, rk4step, pendulum_dxdt, 0.001)

setangle!(p2,[0.1,0.3])

pendulum_basic(Scene (600px, 450px):
  0 Plots
  1 Child Scene:
    └ Scene (600px, 450px), Axis (2 plots), Observable(Float32[0.099833414, -0.9950042]), Observable(Point{2, Float32}[[0.0, 0.0], [0.099833414, -0.9950042]]), [0.1, 0.3], 0.0, 0.01, rk4step, pendulum_dxdt, 0.001)

We can now make a function which steps the pendulum one timestep

function step!(p::abstractpendulum)
    θv=p.step(p.θv,p.dxdt,p.t,p.dt)
    setangle!(p,θv)
    p.t+=p.dt
end

step! (generic function with 1 method)

for i in 1:1000
    step!(p2)
    sleep(p2.delay)
end

One fun thing would be to be able to drag around the pendulum. GLMakie has the ability to watch for mouse clicks.

spoint = select_point(p2.ax.scene, marker = :circle)

function θvcoords(x, y)
    θ = atan(y,x) + π/2
    return [θ,0]
end

on(spoint) do z
    x, y = z
    θv = θvcoords(x, y)
    setangle!(p2,θv)
end

ObserverFunction defined at In[15]:9 operating on Observable(Float32[0.0, 0.0])

for i in 1:1000
    step!(p2)
    sleep(p2.delay)
end

That is fun. Lets update our pendulum constructor so that the object will automatically have that ability.

function pendulum_basic(;θv=[pi/4,0.],t=0,dt=0.01,step=rk4step,dxdt=pendulum_dxdt,delaytime=0.001)
    # Extract positions of pendulum
    θ,v=θv
    x,y=xycoords(θv)
    # Make observables
    ball= Observable(Point2f(x,y))
    rod=Observable([Point2f(0, 0), Point2f(x, y)])
    # Make scene
    fig = Figure(); display(fig)
    ax = Axis(fig[1,1])
    scatter!(ax, ball; marker = :circle, strokewidth = 2, 
        strokecolor = :purple,
        color = :black, markersize = 8)
    lines!(ax, rod; linewidth = 4, color = :purple)
    ax.title = "pendulum"
    ax.aspect = DataAspect() # Set aspect ratio
    xlims!(ax, -1.05, 1.05)
    ylims!(ax, -1.05, 1.05)
    #Create object
    p=pendulum_basic(fig,ax,ball,rod,θv,t,dt,step,dxdt,delaytime) 
    #
    # New lines
    # Set up interactive
    #
    Makie.deactivate_interaction!(ax, :rectanglezoom)
    spoint = select_point(ax.scene, marker = :circle)
    on(spoint) do z
        x, y = z
        θv = θvcoords(x, y)
        setangle!(p,θv)
    end
    return p
end

pendulum_basic

p1=pendulum_basic()

pendulum_basic(Scene (600px, 450px):
  0 Plots
  1 Child Scene:
    └ Scene (600px, 450px), Axis (3 plots), Observable(Float32[0.70710677, -0.70710677]), Observable(Point{2, Float32}[[0.0, 0.0], [0.70710677, -0.70710677]]), [0.7853981633974483, 0.0], 0, 0.01, rk4step, pendulum_dxdt, 0.001)

for i in 1:1000
    step!(p1)
    sleep(p1.delay)
end

Now what we need to do is make a “run” button. That toggles the simulation on and off

isrunning = Observable(false)
label = map(cond -> cond ? "Stop" : "Run", isrunning)
run = Button(p1.fig[2,1]; label = label, tellwidth = false)
on(run.clicks) do clicks; isrunning[] = !isrunning[]; end

ObserverFunction defined at In[20]:4 operating on Observable{Any}(0)

Now lets hook into that observable

isrunning_notifier = Condition()
on(cond -> cond && notify(isrunning_notifier), isrunning)
errormonitor(@async while true
    if isrunning[]
        isopen(p1.fig.scene) || break # ensures computations stop if closed window
        step!(p1)
        sleep(p1.delay) # or `yield()` instead
    else
        wait(isrunning_notifier)
    end
end)

Task (runnable) @0x0000000134b63210

Now lets add that ability to the object – and also copy all of the definitions to one place. This one cell is self-contained, you should be able to run it without any of the rest of the notebook. We need to add new attributes to the object, so we need to rename it.

using GLMakie

function pendulum_dxdt(x,t)
    (theta,v)=x
    return [v,-sin(theta)]
end

function rk4step(x,dxdt,t,deltat)
    k1=dxdt(x,t)
    k2=dxdt(x+k1*(deltat/2),t+deltat/2)
    k3=dxdt(x+k2*(deltat/2),t+deltat/2)
    k4=dxdt(x+k3*deltat,t+deltat)
    return x+(k1+2*k2+2*k3+k4)*(deltat/6)
end

rk4step(;x,dxdt,t,deltat)=rk4step(x,dxdt,t,deltat)

function xycoords(θv)
    θ,v=θv
    return (sin(θ),-cos(θ))
end

function θvcoords(x, y)
    θ = atan(y,x) + π/2
    return [θ,0]
end

abstract type abstractpendulum end

function step!(p::abstractpendulum)
    θv=p.step(p.θv,p.dxdt,p.t,p.dt)
    setangle!(p,θv)
    p.t+=p.dt
end

function setangle!(p::abstractpendulum,θv)
    p.θv=θv
    x,y=xycoords(θv)
    p.rod[] = [Point2f(0, 0), Point2f(x, y)]
    p.ball[] = Point2f(x, y)
    p
end

mutable struct pendulum <:abstractpendulum
    fig #Makie figure object
    ax  #Makie axis object
    ball #Observable corresponding to ball
    rod #Observable corresponding to rod
    θv #vector [θ,v]
    t
    dt
    step  #the stepper for our differential equation solver -- same syntax as rk4step
    dxdt  #the derivitive rule -- same systax as pendulum_dxdt
    delay #how long to wait between displaying frames
    #
    # New lines
    run #button
    isrunning #is the simulation running?
end

# constructor
function pendulum(;θv=[pi/4,0.],t=0.,dt=0.01,step=rk4step,dxdt=pendulum_dxdt,delaytime=0.001)
    # Extract positions of pendulum
    θ,v=θv
    x,y=xycoords(θv)
    # Make observables
    ball= Observable(Point2f(x,y))
    rod=Observable([Point2f(0, 0), Point2f(x, y)])
    # Make scene
    fig,ax=newscene(ball,rod)
    # run button
    run,isrunning=makebutton(fig)
    #Create object
    p=pendulum(fig,ax,ball,rod,θv,t,dt,step,dxdt,delaytime,run,isrunning)
    # Set up interactive
    clicktomove(p)
    startsim(p)   
    return p
end

function newscene(ball,rod)
    fig = Figure(); display(fig)
    ax = Axis(fig[1,1])
    scatter!(ax, ball; marker = :circle, strokewidth = 2, 
        strokecolor = :purple,
        color = :black, markersize = 8)
    lines!(ax, rod; linewidth = 4, color = :purple)
    ax.title = "pendulum"
    ax.aspect = DataAspect() # Set aspect ratio
    xlims!(ax, -1.05, 1.05)
    ylims!(ax, -1.05, 1.05)
    return fig,ax
end

function makebutton(fig)
    isrunning = Observable(false)
    label = map(cond -> cond ? "Stop" : "Run", isrunning)
    run = Button(fig[2,1]; label = label, tellwidth = false)
    on(run.clicks) do clicks; isrunning[] = !isrunning[]; end
    return run,isrunning
end

function clicktomove(p::abstractpendulum)
    ax=p.ax
    Makie.deactivate_interaction!(ax, :rectanglezoom)
    spoint = select_point(ax.scene, marker = :circle)
    on(spoint) do z
        x, y = z
        θv = θvcoords(x, y)
        setangle!(p,θv)
    end
end
    
function startsim(p::abstractpendulum)
    isrunning_notifier = Condition()
    on(cond -> cond && notify(isrunning_notifier), p.isrunning)
        errormonitor(@async while true
        if p.isrunning[]
            isopen(p.fig.scene) || break # ensures computations stop if closed window
            step!(p)
            sleep(p.delay) # or `yield()` instead
        else
            wait(isrunning_notifier)
        end
    end)
end

startsim (generic function with 1 method)

p3=pendulum()

pendulum(Scene (600px, 450px):
  0 Plots
  2 Child Scenes:
    ├ Scene (600px, 450px)
    └ Scene (600px, 450px), Axis (3 plots), Observable(Float32[0.70710677, -0.70710677]), Observable(Point{2, Float32}[[0.0, 0.0], [0.70710677, -0.70710677]]), [0.7853981633974483, 0.0], 0.0, 0.01, rk4step, pendulum_dxdt, 0.001, Button(), Observable(false))

Adding trails#

Now this is just eye candy

using DataStructures: CircularBuffer

A circular buffer is a data type which is like a list or vector – but when add elements on the end it pushes them off the other

cb=CircularBuffer{typeof(1.)}(3)
fill!(cb,1.)

3-element CircularBuffer{Float64}:
 1.0
 1.0
 1.0

push!(cb,2.)

3-element CircularBuffer{Float64}:
 1.0
 1.0
 2.0

push!(cb,3.)

3-element CircularBuffer{Float64}:
 1.0
 2.0
 3.0

push!(cb,4.)

3-element CircularBuffer{Float64}:
 2.0
 3.0
 4.0

Make a circular buffer which will store the past locations of the pendulum bob.

tail = 300
traj = CircularBuffer{Point2f}(tail)
x,y=xycoords(p3.θv)
fill!(traj, Point2f(x, y))
traj = Observable(traj); # make it an "Observable" -- meaning GLMakie will update the graph if it is changed

Make a list of colors which will fade from white to purple. Then add the trail to the plot

c = to_color(:purple)
tailcol = [RGBAf(c.r, c.g, c.b, (i/tail)^2) for i in 1:tail]
lines!(p3.ax, traj; linewidth = 3, color = tailcol)

Lines{Tuple{CircularBuffer{Point{2, Float32}}}}

Now lets upgrade the setangle command so that it also updates the trail

function setangle!(p::abstractpendulum,θv)
    p.θv=θv
    x,y=xycoords(θv)
    p.rod[] = [Point2f(0, 0), Point2f(x, y)]
    p.ball[] = Point2f(x, y)
    push!(traj[], Point2f(x, y))
    notify(traj) # needed to tell GLMakie that we updated traj -- push! doesn't send that signal
    p
end

setangle! (generic function with 2 methods)

for i in 1:500
    step!(p3)
    sleep(p3.delay)
end

Now lets encapsulate that. Again, I repeated all of the definitions, so that it is self-contained. Again we need to rename the object, or restart the kernel, because we need to add attributes.

using GLMakie
using DataStructures: CircularBuffer

function pendulum_dxdt(x,t)
    (theta,v)=x
    return [v,-sin(theta)]
end

function rk4step(x,dxdt,t,deltat)
    k1=dxdt(x,t)
    k2=dxdt(x+k1*(deltat/2),t+deltat/2)
    k3=dxdt(x+k2*(deltat/2),t+deltat/2)
    k4=dxdt(x+k3*deltat,t+deltat)
    return x+(k1+2*k2+2*k3+k4)*(deltat/6)
end

rk4step(;x,dxdt,t,deltat)=rk4step(x,dxdt,t,deltat)

function xycoords(θv)
    θ,v=θv
    return (sin(θ),-cos(θ))
end

function θvcoords(x, y)
    θ = atan(y,x) + π/2
    return [θ,0]
end


abstract type abstractpendulum end

function step!(p::abstractpendulum)
    θv=p.step(p.θv,p.dxdt,p.t,p.dt)
    setangle!(p,θv)
    p.t+=p.dt
end

mutable struct pendulum_fancy <:abstractpendulum
    fig #Makie figure object
    ax  #Makie axis object
    ball #Observable corresponding to ball
    rod #Observable corresponding to rod
    traj #Observable corresponding to rod
    θv #vector [θ,v]
    t #current time
    dt #time step
    step
    dxdt
    delay #how long to wait between displaying frames
    run #button
    isrunning #is the simulation running?
end

function pendulum_fancy(;θv=[pi/4,0.],t=0.,dt=0.01,step=rk4step,dxdt=pendulum_dxdt,delaytime=0.001,tail=300)
    # Extract positions of pendulum
    θ,v=θv
    x,y=xycoords(θv)
    # Make observables
    ball= Observable(Point2f(x,y))
    rod=Observable([Point2f(0, 0), Point2f(x, y)])
    # Make scene
    fig,ax=newscene(ball,rod)
    # run button
    run,isrunning=makebutton(fig)
    # Now lets make the trail
    traj=maketrail(ax,tail)
    #=
    traj = CircularBuffer{Point2f}(tail)
    fill!(traj, Point2f(x, y))
    traj = Observable(traj)
    c = to_color(:purple)
    tailcol = [RGBAf(c.r, c.g, c.b, (i/tail)^2) for i in 1:tail]
    lines!(ax, traj; linewidth = 3, color = tailcol)
    =#
    #Create object
    p=pendulum_fancy(fig,ax,ball,rod,traj,θv,t,dt,step,dxdt,delaytime,run,isrunning)
    # Set up interactive
    clicktomove(p)
    #animation
    startsim(p)   
    return p
end

function setangle!(p::pendulum_fancy,θv)
    p.θv=θv
    x,y=xycoords(θv)
    p.rod[] = [Point2f(0, 0), Point2f(x, y)]
    p.ball[] = Point2f(x, y)
    push!(p.traj[], Point2f(x, y))
    notify(p.traj) # needed to tell GLMakie that we updated traj -- push! doesn't send that signal
    p
end

function newscene(ball,rod)
    fig = Figure(); display(fig)
    ax = Axis(fig[1,1])
    scatter!(ax, ball; marker = :circle, strokewidth = 2, 
        strokecolor = :purple,
        color = :black, markersize = 8)
    lines!(ax, rod; linewidth = 4, color = :purple)
    ax.title = "pendulum"
    ax.aspect = DataAspect() # Set aspect ratio
    xlims!(ax, -1.05, 1.05)
    ylims!(ax, -1.05, 1.05)
    return fig,ax
end

function makebutton(fig)
    isrunning = Observable(false)
    label = map(cond -> cond ? "Stop" : "Run", isrunning)
    run = Button(fig[2,1]; label = label, tellwidth = false)
    on(run.clicks) do clicks; isrunning[] = !isrunning[]; end
    return run,isrunning
end

function maketrail(ax,tail)
    traj = CircularBuffer{Point2f}(tail)
    fill!(traj, Point2f(x, y))
    traj = Observable(traj)
    c = to_color(:purple)
    tailcol = [RGBAf(c.r, c.g, c.b, (i/tail)^2) for i in 1:tail]
    lines!(ax, traj; linewidth = 3, color = tailcol)
    return traj
end

function clicktomove(p::abstractpendulum)
    ax=p.ax
    Makie.deactivate_interaction!(ax, :rectanglezoom)
    spoint = select_point(ax.scene, marker = :circle)
    on(spoint) do z
        x, y = z
        θv = θvcoords(x, y)
        setangle!(p,θv)
    end
end

function startsim(p::abstractpendulum)
    isrunning_notifier = Condition()
    on(cond -> cond && notify(isrunning_notifier), p.isrunning)
        errormonitor(@async while true
        if p.isrunning[]
            isopen(p.fig.scene) || break # ensures computations stop if closed window
            step!(p)
            sleep(p.delay) # or `yield()` instead
        else
            wait(isrunning_notifier)
        end
    end)
end

startsim (generic function with 1 method)

p4=pendulum_fancy()

pendulum_fancy(Scene (600px, 450px):
  0 Plots
  2 Child Scenes:
    ├ Scene (600px, 450px)
    └ Scene (600px, 450px), Axis (4 plots), Observable(Float32[0.70710677, -0.70710677]), Observable(Point{2, Float32}[[0.0, 0.0], [0.70710677, -0.70710677]]), Observable(Point{2, Float32}[[0.70710677, -0.70710677], [0.70710677, -0.70710677], [0.70710677, -0.70710677], [0.70710677, -0.70710677], [0.70710677, -0.70710677], [0.70710677, -0.70710677], [0.70710677, -0.70710677], [0.70710677, -0.70710677], [0.70710677, -0.70710677], [0.70710677, -0.70710677]  …  [0.70710677, -0.70710677], [0.70710677, -0.70710677], [0.70710677, -0.70710677], [0.70710677, -0.70710677], [0.70710677, -0.70710677], [0.70710677, -0.70710677], [0.70710677, -0.70710677], [0.70710677, -0.70710677], [0.70710677, -0.70710677], [0.70710677, -0.70710677]]), [0.7853981633974483, 0.0], 0.0, 0.01, rk4step, pendulum_dxdt, 0.001, Button(), Observable(false))
Contents