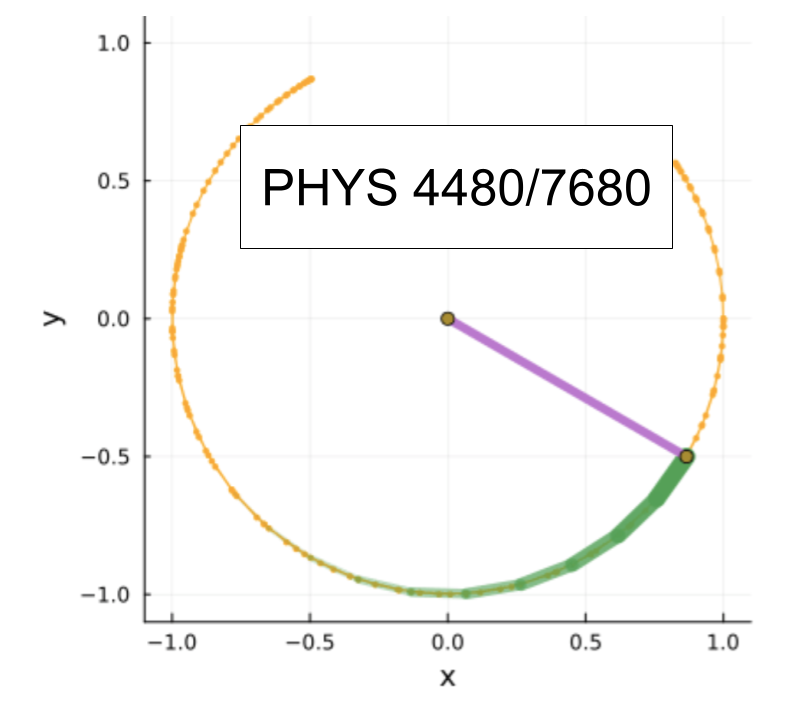
Exploring Chaos with our Duffing Simulator#
Here is my version of the Duffing Simulator. I added a few extra bells and whistles, but it is essentially the function you wrote in class.
New elements:
I draw the potential surface
When you click, you produce not only an oscillator with the parameters corresponding to that point, but a whole ring of initial conditions around it.
I have sliders to control everything.
Note: I put pretty much everything in my constructor as one monolithic block. It makes more sense to do it like we did with the pendulum, and write functions that do each piece.
using GLMakie
using DataStructures: CircularBuffer
using LaTeXStrings
mutable struct duffing
# Basic Scene info
fig # the Makie Figure object
ax # the Makie Axis object
# Time evolution info
xv # the phase space position of the oscillator
t # the current time
dt # the step size
step # our stepper -- we will use rk4step as the default
dxdt # the derivitive rule
p # parameters of the differential equation -- a struct
# with field F,ω,α,β,γ
# UI features
delay # how long to wait between frames
ball # the observable which will be plotted
traj # stores past points for drawing a "tail"
ptraj # not used
sliders # named tuple of UI elements to control force and frequency
# Can again use the same struct that we used for p,
# with attributes F,ω,α,β,γ
run # button to turn on and off animation
isrunning # is simulation running?
potential # stored values of the potential for plotting
grad # stored values of the gradient for plotting
bg
burst
end
mutable struct dp
F ::Float64
ω ::Float64
α ::Float64
β ::Float64
γ ::Float64
end
dp(;F,ω,α,β,γ)=dp(F,ω,α,β,γ)
function rk4step(x,p,dxdt,t,deltat)
k1=dxdt(x,p,t)
k2=dxdt(x+k1*(deltat/2),p,t+deltat/2)
k3=dxdt(x+k2*(deltat/2),p,t+deltat/2)
k4=dxdt(x+k3*deltat,p,t+deltat)
return x+(k1+2*k2+2*k3+k4)*(deltat/6)
end
function duf_dxvdt(xv,p,t)
x,v = xv
return[v,-2*p.γ*v-p.α*x-p.β*x^3+p.F*cos(p.ω*t)]
end
function setxv!(d::duffing,xv)
d.xv=xv
d.ball[]=Point2f(xv...)
push!(d.traj[], Point2f(xv...))
notify(d.traj) # needed to tell GLMakie that we updated traj -- push! doesn't send that signal
d
end
function step!(d::duffing)
xv=d.step(d.xv,d.p,d.dxdt,d.t,d.dt)
setxv!(d,xv)
d.t+=d.dt
p=d.p
F=p.F
t=d.t
ω=p.ω
d.bg[]=d.potential-F*cos(ω*t).*d.grad
d.burst[]=[d.step(w,d.p,d.dxdt,d.t,d.dt) for w in d.burst[]]
d
end
function duffing(;
xv=[0.5,0.],
p=dp(α=-1,β=1,γ=0.1,F=0.,ω=1.),
t=0.,
dt=0.02,
delay=0.00001,
step=rk4step,
dxdt=duf_dxvdt,tail=300)
# Create Figure object
#
fig = Figure(); display(fig)
ax = Axis(fig[1,1])
ax.title = "Duffing"
ax.aspect = DataAspect()
# create background
xlist=range(-2,2,100)
ylist=range(-2,2,100)
potential=[p.α*x^2/2+p.β*x^4/4+y^2/2 for x in xlist, y in ylist];
grad=[x for x in xlist, y in ylist];
bg=Observable(potential+0. .* grad);
image!(ax,(-2,2),(-2,2),bg,colormap=[:white,:red,:yellow,:magenta])
contour!(ax,(-2,2),(-2,2),bg,levels=20)
#
# Create ball object, and add it to scene
#
ball=Observable(Point2f(xv...))
scatter!(ax, ball; marker = :circle, strokewidth = 2,
strokecolor = :purple,
color = :black, markersize = 8)
# run button
# run button
isrunning = Observable(false)
label = map(cond -> cond ? "Stop" : "Run", isrunning)
run = Button(fig[2,1]; label = label, tellwidth = false)
on(run.clicks) do clicks; isrunning[] = !isrunning[]; end
# Make Sliders
Label(fig[1,2][1,1],L"\frac{dv}{dt}=-2\gamma v-\alpha x-\beta x^3 +F \cos(\omega t).")
sg=SliderGrid(fig[1,2][2,1],
(label="F",range=0.:0.01:1.,format = "{:.2f}",startvalue=p.F),
(label="ω",range=0.01:0.01:2,format = "{:.2f}",startvalue=p.ω),
(label="γ",range=0.0:0.01:1,format = "{:.2f}",startvalue=p.γ),
width=200,tellheight=false)
Fobserver=sg.sliders[1].value;
ωobserver=sg.sliders[2].value;
γobserver=sg.sliders[3].value;
on(Fobserver) do Fobserver
p.F=Fobserver[]
end
on(ωobserver) do ωobserver
p.ω=ωobserver[]
end
on(γobserver) do γobserver
p.γ=γobserver[]
end
sg2=SliderGrid(fig[1,2][3,1],
(label="α",range=-2.:0.01:2.,format = "{:.2f}",startvalue=p.α),
(label="β",range=0.:0.01:1.,format = "{:.2f}",startvalue=p.β),
width=200,tellheight=false)
αobserver=sg2.sliders[1].value;
βobserver=sg2.sliders[2].value;
sg3=SliderGrid(fig[2,2],
(label="dt",range=0.:0.002:0.2,format = "{:.2f}",startvalue=dt),
width=200,tellheight=false)
dtobserver=sg3.sliders[1].value;
# code moved below instantiation
# Now lets make the trail
traj = CircularBuffer{Point2f}(tail)
fill!(traj, Point2f(xv...))
traj = Observable(traj)
c = to_color(:purple)
tailcol = [RGBAf(c.r, c.g, c.b, (i/tail)^2) for i in 1:tail]
lines!(ax, traj; linewidth = 3, color = tailcol)
#Burst
burst=Observable([Point2f(xv[1]+0.1*cos(θ),xv[2]+0.1*sin(θ)) for θ in 0.:2*pi/1000:2*pi])
scatter!(ax,burst)
#Create object
d= duffing(
fig #= the Makie Figure object that you created=#,
ax #= the Makie Axis object that you created=#,
xv #= initial conditions passed from constructor=#,
t #= the current time passed from constructor=#,
dt #= the step size passed from constructor=#,
step #= our stepper passed from constructor=#,
dxdt #= the derivitive rule passed from constructor=#,
p #= passed from constructor=#,
delay #= passed from constructor=#,
ball #= the observable that you created =#,
traj #=traj=#,
[] #=ptraj -- empty list =#,
sg #=sliders =#,
run #=run =#,
isrunning #=isrunning=#,
potential #=potential=#,
grad #=gradient=#,
bg,burst)
on(dtobserver) do dtobserver
d.dt=dtobserver[]
end
on(αobserver) do αobserver
p.α=αobserver[]
xlist=range(-2,2,100)
ylist=range(-2,2,100)
d.potential=[p.α*x^2/2+p.β*x^4/4+y^2/2 for x in xlist, y in ylist];
end
on(βobserver) do βobserver
p.β=βobserver[]
xlist=range(-2,2,100)
ylist=range(-2,2,100)
d.potential=[p.α*x^2/2+p.β*x^4/4+y^2/2 for x in xlist, y in ylist];
end
# Set up interactive
Makie.deactivate_interaction!(ax, :rectanglezoom)
spoint = select_point(ax.scene, marker = :circle)
on(spoint) do z
setxv!(d,z)
burst[]=[Point2f(z[1]+0.1*cos(θ),z[2]+0.1*sin(θ)) for θ in 0.:2*pi/1000:2*pi]
end
startsim(d)
xlims!(ax,-2,2)
ylims!(ax,-2,2)
#
return d
end
function startsim(p::duffing)
isrunning_notifier = Condition()
on(cond -> cond && notify(isrunning_notifier), p.isrunning)
errormonitor(@async while true
if p.isrunning[]
isopen(p.fig.scene) || break # stops if window is closed
step!(p)
sleep(p.delay)
else
wait(isrunning_notifier)
end
end)
end
startsim (generic function with 1 method)
d1=duffing()
duffing(Scene(6 children, 0 plots), Axis (6 plots), [0.5, 0.0], 0.0, 0.02, rk4step, duf_dxvdt, dp(0.0, 1.0, -1.0, 1.0, 0.1), 1.0e-5, Observable(Float32[0.5, 0.0]), Observable(Point{2, Float32}[[0.5, 0.0], [0.5, 0.0], [0.5, 0.0], [0.5, 0.0], [0.5, 0.0], [0.5, 0.0], [0.5, 0.0], [0.5, 0.0], [0.5, 0.0], [0.5, 0.0] … [0.5, 0.0], [0.5, 0.0], [0.5, 0.0], [0.5, 0.0], [0.5, 0.0], [0.5, 0.0], [0.5, 0.0], [0.5, 0.0], [0.5, 0.0], [0.5, 0.0]]), Any[], SliderGrid(), Button(), Observable(false), [4.0 3.9200081624324046 … 3.9200081624324046 4.0; 3.7664231813746545 3.6864313438070595 … 3.6864313438070595 3.7664231813746545; … ; 3.7664231813746545 3.6864313438070595 … 3.6864313438070595 3.7664231813746545; 4.0 3.9200081624324046 … 3.9200081624324046 4.0], [-2.0 -2.0 … -2.0 -2.0; -1.9595959595959596 -1.9595959595959596 … -1.9595959595959596 -1.9595959595959596; … ; 1.9595959595959596 1.9595959595959596 … 1.9595959595959596 1.9595959595959596; 2.0 2.0 … 2.0 2.0], Observable([4.0 3.9200081624324046 … 3.9200081624324046 4.0; 3.7664231813746545 3.6864313438070595 … 3.6864313438070595 3.7664231813746545; … ; 3.7664231813746545 3.6864313438070595 … 3.6864313438070595 3.7664231813746545; 4.0 3.9200081624324046 … 3.9200081624324046 4.0]), Observable(Point{2, Float32}[[0.6, 0.0], [0.599998, 0.0006283144], [0.5999921, 0.001256604], [0.59998226, 0.0018848439], [0.59996843, 0.0025130096], [0.5999507, 0.0031410758], [0.599929, 0.0037690182], [0.5999033, 0.004396812], [0.5998737, 0.0050244317], [0.59984016, 0.0056518535] … [0.59984016, -0.0056518535], [0.5998737, -0.0050244317], [0.5999033, -0.004396812], [0.599929, -0.0037690182], [0.5999507, -0.0031410758], [0.59996843, -0.0025130096], [0.59998226, -0.0018848439], [0.5999921, -0.001256604], [0.599998, -0.0006283144], [0.6, -2.4492935f-17]]))
## In-Class Activity 1
Everyone in class should start this running. Get in groups of 2 and play with the following. I’ll have one or two groups explain what they saw afterwards.
Set \(\alpha=1,\beta=0,F=0,\gamma=0\). This is the simple harmonic oscillator. How does it behave?
Turn on \(\gamma\), how does that change the behavior?
Now turn on \(F\). You can increase/decrease the timestep to speed up or slow down the motion. Can you see resonant behavior? What happens when \(\omega\) is very small? Very big?
## In-Class Activity 2
Now set \(\alpha=-1,\beta=1,F=0,\omega=1, \gamma=0\). There are 3 types of trajectories: Those that circle \((x,v)=(1,0)\), those that circle \((x,v)=(0,1)\), and those that circle both points.
Turn on \(\gamma\). What happens to each of those 3 types of trajectories? Click on different starting points, and see what the “basins of attraction” are for the various fixed points. You can change
dtto speed up or slow down the smulation.Now turn on a weak driving. Try \(F=0.1,\gamma=0.07\). Up the timestep so that the transients decay quickly. How many different stable orbits can you find? I found 4.
Increase \(F\) to \(0.2\). The transients should start to get interesting. Run with a fast time-step to see if they die out.
Now go to \(F=0.29\). You should get chaotic behavior here (at least for the right initial conditions). What is happening with the blue points? Can you come up with a story about what is happening with the phase space volume? Does this shed light on the “strange attractor” that you saw in the Poincare section?
## In-Class Activity 3
If you set the parameters just right, one can find regular trajectories whose period is a multiple of the drive period. The following gave me a trajectory whose period is twice the drive period: \(F=0.32,\omega=1.4,\gamma=0.05,\alpha=-1,\beta=1\). You might need to make a large timestep for a while to get rid of the transients. You may also need to try a couple initial conditions.
If I go to \(F=0.34\) I get one whose period is 4 times the drive period. To see it, up the timestep, so that the trails outline the whole multiple loop trajectory.
This is the “period doubling” route to chaos. As one approaches the chaotic point the periods get longer and longer, until they are infinite.